Quantum computers are an important discovery and they will have equally important impact on human knowledge as the invention of electricity or radioactivity had. This is so (especially) because even smaller quantum computer has potentially larger computational effect than all computers in the world combined! Where does a quantum computer (QC) take a billion times multiple of classical computer’s power? Is it possible for it to run completely without electricity? Are QC’s universal or useful only in a narrow industry? Which professions working with the computer today should eye a quantum computer, and whom would the QC evade for the rest of their lives? All of the above (and a bit more) you should find out in the following lines.
Classical Computer (CC) vs. Quantum computer (QC): Can we tell them apart?
Try to think for a moment: What do you know about Quantum Computers? When I asked colleagues and other people in my surroundings about what they knew about quantum computers, they mostly told me that: 1] they’re faster, faster than Classical computers, but they haven’t yet mushroomed (for unknown reasons), probably too expensive (?) and they are being worked on only in research departments of universities and major digital Titans (like Google or Amazon); 2] Their performance is measured not in GigaHerz, but in weird Qubit units; (what is it?) 3] They use some kind of quantum physics and so it’s complicated enough that nobody actually understands how they work; 4] They can calculate things that we cannot otherwise calculate (but no one can name any specific one). And that is the end of the line, usually. If I were to summarize it into single sentence, I would probably say that general (or even expert) public currently perceives quantum computers as: “Complex, particle physics-based black box that counts faster, but few understand it and thus it is not yet wide-spread.” Well, my hope is that after finishing this article, you will also condescendingly lough at this answer. It is the very shallow actual knowledge of such an important technology that made me write this blog.
The essence of Quantum computers indeed is stemming from laws and processes of Quantum mechanics, the branch of physics that we really mean when we utter “… we do it quickly, it’s not nuclear physics!” Quantum mechanics really is such a complex branch of physics that lending quote from famous Czech movie ‘Jak basnikum chutna zivot‘ [How Poets’ Lives Taste] : “Only God knows the subject for A, the Nobel Prize winner for B or C, the university professors for D, their best students might score E and its (F)AIL for everyone else! ” (disclaimer: in the original film, the statement was about Chemistry). As a result, when you open a book on QC, complicated physics formulas and equations (on which my undergraduate roommate jokingly remarked: “Filip, I have been redrawing the figures the whole lecture, because you can only take notes, if you know what you are writing about“) overwhelm you on the very first pages. Consequently, the understanding of QC (and their use) narrows for most of us to the few sentences of the previous paragraph.
And pity it is. Yes, QC can be (quite densely) discussed in the form of complicated schemes and formulas. But it can be done differently, too. And is this blog-post’s mission: To give you the essence of quantum computers without complicated equations and without assuming that you have passed the exam on differential equations or linear algebra. If it still fails to do so, I apologize in advance. However, it would be nice if you to give me after reading a short feedback (to info@mocnedata.sk) on whether it succeeded in doing so. Last thing before we start, let me do a short disclaimer: Although I have successfully passed the above tests and are therefore have privilege of comprehending the complicated equations, I do not make Quantum Mechanics for living. Therefore, if you are a researcher in this area, forgive me the simplifications made in the next paragraphs. They stem from either trying to be readable to wider masses or from the fact that some nitty-gritty’s are beyond my own power. (after all, I’m not a Nobelist nor a college professor :))
Where it all had started
Many of the areas of science that even a primary school pupil can master nowadays have not been known for thousands of years of human existence. For example, such trivial things as -400 (negative numbers) have long been beyond the understanding of not only ordinary people but also contemporary scientists. (Seriously: have you ever seen a negative number in Roman numerals?) The reason was that back then people used mathematics (and other sciences) for practical purposes only. And until the invention of accounting, the negative number had no point in life. In common life you simply cannot see -5 apples. One of those mathematics areas “only destined for selected few” were complex numbers. Even René Descartes spoke of them with mockery, and it was only thanks to scientists like Gauss or Euler that they have made it to the Earth. As complex numbers are an important building block of quantum computers, let me briefly approach them here. They will be very instrumental for understanding the “distinctness” of QC.
Mathematics has been associated with the solution of equations since ancient times. While we, as humanity, counted only simple equations of 1 variable, each equation had a solution (or clear evidence that it could not have one). However, when we went into the calculations with circles (and other conic curves), we found that some of our equations suddenly had no solution (and it wasn’t even obvious why they shouldn’t have them). For example, the simple quadratic equation x ^ 2 + 2 = 1 (which we all learned to solve, and therefore I give it here as an example) does not have a solution in the set of real numbers, since the solution would have to be the square root of -1 (because x ^ 2 = -1). And that cannot be calculated. Or can it?
In ancient Greece, the square root was defined (by Pythagoras) as the diagonal of the rectangle (e.g. the square root of 5 is the diagonal of the rectangle with sides of 1 and 2) and each line ( even diagonal) must be larger than zero. This burden has been on our shoulders for more than 2,000 years, until someone said: What if we imagined an virtual (third) dimension in which any 2D object could be rotated by some angle. Like an arrow drawn from the center out on the right page of a book with thin, translucent leaves. As you turn the page of the book, the same arrow suddenly – though it has not changed at all – points in the opposite direction (from center to left). If we take the arrow as a shift on the map by 1 length unit from point A to B, after reversing suddenly we have a shift of -1 (that is the same length, but in the opposite direction). Somewhat analogically, a diagonal of a square root of -1 can be formed. It is the angle of rotation in the imaginary third dimension that is the essence of complex numbers. In order to make it easier to calculate, a unit of rotation (= a quarter of circle rotation) has been chosen, which (after some trigonometric transformation) is labeled as a lower case “i”.
Here we can abruptly stop our short trip to mathematics, as the “hiking track” further continues through ugly cosines, sines and large matrices. However, two more things are important for our further discussion of quantum computers:
A] There is infinity of angles under which I can gradually turn the page of the book, each rotation resulting into rectangle’s diagonal of a “different length”. Thus, if I start to rotate (and connect) simple things in an imaginary space, the (computational) difficulty in determining all possible states of rotation steeply increases.
B] In physics (especially quantum physics) some objects (namely small particles) actually behave in a way that fits the domain of complex numbers. Thus, what began as an human urge to find a solution for each quadratic equation, later has proved to be truly useful for describing the real life of nature around us.
OK. But what role do complex numbers play in quantum computers?
The main “weapons” of Quantum computers
Most of us use classical computers somewhat naturally. We are used to take a laptop and open it on a train or airplane. The notebook (unless it has run out of battery) obediently executes any calculation command. Since most common users’ needs are a “piece of cake” for the ever-increasing performance of computer hardware, you probably never thought about the operational limits of a classical computer (maybe beyond the laptop battery). Although we are experiencing a golden age of computer development, and under (unwritten) Moore’s law, the performance and memory capabilities of available computers are literally multiplying year on year, there is indeed a physical limit of computers. For conventional conventional computers to run they need to rewrite ones in the memory to zeros and back. The smallest unit of their memory is called BIT. (The byte and thus the mega- or giga-byte are somewhat larger cousins of BIT). The so-called Lendauer’s bound determines the minimum amount of energy required to overwrite one bit. Thus, nature had set a strict limit on what is the least amount of energy (read electricity) it costs to count things. When we hit this limit, we will no longer be able to increase the performance of computers in other way than “burning” more electricity. And since our electricity sources are limited, we will inevitably encounter an upper limit of computing power one point in time. Although this upper limit will never bother us for our trivial tasks (like watching a video or sending an email), there are already scientific calculations (mostly in space and encryption areas) that have indeed already encountered theoretical limits of classical computer calculations. If we, as humanity, want to bypass the physical ceiling of classical computers in future, we have to come up with a computer that can count without having to rewrite zeros and ones. This is exactly what Quantum computers can.
The second significant limit of classical computers is that when calculating (e.g. multiplying) they must first store all the inputs (numbers that they multiply), then use the free parts of memory to perform the calculation (something like multiplying beneath each other on paper) and finally save the result of the calculation (the final product) in another part of the memory. Even worse, if you want to check your computer, you must save all the inputs and outputs of the calculations, otherwise you won’t be able to look back whether the result is actually the correct product of the numbers. This brings the limitation that a considerable part of the memory (and performance) of a conventional computer is continually tied to storing the already executed (or currently running) steps in order to track their progress. Alternatively, to ensure that the computer will be able to resume the task if something interrupted it. The reason why classical computers have been designed this way is that it allows them to theoretically calculate any computational task. However, the down side of this design is that calculations where computational demands grow exponentially (insiders know geometrically is enough even) with the number of inputs (such as lotteries or sorting things) cease to be realistic. Password protection is a good example. Each password can be broken by “blunt” trying all options around. However, if you have a sufficiently long (and varied) password, it can take years to decades to break it down. So it is maintained that by the time that someone breaks it you would have changed your password already anyway. But what if there was a new type of computer that does not need to keep continuous inputs and can jump from typing straight to result? Sounds like magic or science fiction? Well, this is how quantum computers work.
With a bit of irony, one could say that we were not ambitious enough in the construction of classical computers (CC). The CCs have been designed in a way that they always deliver only one alternative result at time. On punch cards (yes, the first computers recorded the result on a paper tape using a pinhole system, something like a primitive version of Braille or a paper woodpecker) one could only write one value at a time (and place). You needed another punch card to write another value. Over time, we have compressed the writing technique so that today we can insert billions of meters of punch tape into a few cubic centimeters of a USB key, but the principle of one value at a time (and at one place) has been preserved. The difference of quantum computers also results from the fact that one QUBIT (quantum BIT) can theoretically represent a huge number of different states (using complex numbers). It represents the physical nature of the particles, which themselves have countless states. The difference dramatically alters QC’s memory requirements, while allowing you to work more efficiently in modeling processes, in which things can end in large variety of states.
How quantum computers actually work
Well, it sounds all pink and incredible. But how does a quantum computer actually work? Is it the same “iron box” we’re used to on our desks? The unit of quantum computer power is QUBIT (= quantum bit). Since QUBIT must predominantly be able to function without a constant supply of electricity (remember the Lendauer constraint), QUBIT has to physically be modeled as an object that can change its state, retain its value and behave according to complex number manipulation rules (as we described in introductory part of the blog). In our physical, real world, atomic particles best meet these requirements. Therefore, although there are more technological approaches to creating QUBIT, the ions, polymer particles, photons, or silicon (and various other) atoms are most common choices. As the size of these particles is at least a million times smaller than the size of smallest conventional PC components, you would fit a very powerful quantum supercomputer under your nail. (spoiler: few lines down you will find out that it would be freezing cold)
The principle of QUBIT itself works in a way that a particle can have different energy levels (e.g. manifested by electric charge, speed of movement or other properties). Using microwave radiation or (laser) light beam, you can “poke” a given particle remotely to gain or lose some energy. If you select energy levels distant enough from each other (which ensures that a particle has almost no chance of moving between the two states on its own), you can use those particle states as zeros and ones in the calculation. Something like having a thermometer in a sealed room and considering a temperature above 80 degrees Celsius as 1 and a temperature below -50 degrees Celsius as 0. (The chance that a room moves from 80 degrees to -50 without your involvement is almost impossible.) The only, but significant, difference is that while moving between 80 and -50 degrees requires a lot of energy, for QUBIT to do the transition particle needs to be only targeted by microwave or light beam (and the same beam can even control multiple QUBITs simultaneously). Of course, the particles move along microscopic paths and at normal temperatures their movement is too quick and chaotic. Thus, to form QUBITs, the particles need to be “calmed down” until an almost absolute cessation of motion occurs, at a temperature (close to) zero Kelvin, or -273.15 degrees Celsius. This makes quantum computers relatively difficult to construct under normal conditions. As the idea of having something with temperature of minus 273 degrees on your desk is probably down right absurd.
Therefore, most quantum computers still work in closed laboratories where maintaining such a low temperature is possible and at least somewhat effective. A quantum laptop laid on the beach or on grass in a meadow doesn’t seem to be a very real idea. However, the fact that the construction of QUBIT requires “atypical” conditions does not exclude us all from the use of QC. Once someone is running a quantum computer, you can “borrow its computing power remotely“. All you have to do is submit a calculation request (along with inputs) from your computer via the Internet (or a private cloud), and the quantum administrator will include your calculation in the task queue. When comes the time for your calculation, the QC starts the script and tells you the result. After all, this was exactly how the big mainframes, where you also had to schedule some machine time, had been used first place.
Now that we know how QUBITs work physically, we need to point out one important contrast to conventional computers. QUBITs are real particles from real life, and although we can enforce at least elementary “obedience” upon them at low temperatures (and with some other measures), there is still a non-zero likelihood that some external influence (or accidental event) will deflect the energy of the particle and the ones turns to zero or the energy level got stuck somewhere between the zero level and the one level. (means, it is unclear whether the operation resulted in zero or one.) Therefore, logical QUBIT principle is used on top to prevent this phenomenon. This works in a way that physical QUBIT has several “siblings” on which the same operations are performed as on the initial QUBIT. The entire group of primary QUBIT and its physical siblings is called logical QUBIT. The value of the logical QUBIT is determined as the value that came out most often on physical QUBITs connected to the given logical QUBIT. That means that even if one of the 1000 physical QUBITs associated in a logical QUBIT is wrong (or its value cannot be detected), the other 999 still offer the same result and serve as a form of insurance. The probability that all 1000 would be wrong in the same direction at the same time is so low that it is completely negligible for the necessary calculations. In addition, if you repeat the calculation several times in sequence, you gain assurance that the quantum computer was not mistaken.
We explained how QUBITs look like. However, we still owe a substantial answer to how QC actually does the calculations. To do this, we need to clarify the concept of a reversible operation. This is a (mathematical) operation in which I can name the original inputs just from the result without the inputs ever being revealed to me. For example, the sum is not a reversible operation, because if you tell me that the sum of two numbers is 7, I cannot tell what two numbers you have added, there are infinitely many possibilities (e.g. -1000 + 1007 = 7). The classic computers we have on our desks today are programmed to do both reversible and irreversible operations. The tax for this is, as already mentioned, the storage needed for inputs and intermediate results. However, quantum computers are designed to perform only reversible operations. For example, multiplication -1 is a reversible operation because I do not need to know what the input was: if I see that the output is -10, I know that the input had to be 10 and only 10. For any other input I do not get -10 after multiplying by -1. Quantum computers thus calculate by taking input, executing a series (= quantum circuit) of reversible operations (also called quantum gates), and returning the result. However, since all operations are reversible, it is easy to chain operations into long sequences. It is also fast to check whether the result of the whole quantum circuit fits with the corresponding inputs. This allows a large number of operations to be performed without any memory requirement. Do you need to multiply two matrices, each with a million elements? No problem, QC can do it “out of its head” without having to make a note of anything. What is more, it does so about as fast as multiplying only one-hundred-elements-matrices with each other.
This specificity of the calculations makes the QC an excellent and ultra-fast solution for some types of calculations and, on the contrary, disadvantaged for some other (even trivial) operations. It is so because most common mathematical operations can be rewritten into a sequence of (several) reversible calculations (for example, if you want to calculate the product 100 x 10 you can take zero and add one hundred units 10 times to it (because +100 operation is reversible). For very large factors this would become obstacle itself rather than a help). So quantum computers are a bit, ehm, autistic. They do brilliant sophisticated things, but for some trivial things they are completely lost. Therefore, your homework from elementary school will probably never be counted on Quantum’s computer. Tasks where the power of QC significantly beats classic computers are tasks with either a huge number of things (e.g. stars, atoms, chemical reactions, …) or a very high number of repetitions of the same procedure (e.g. verifying if a number is not a prime number by trying to divide it by all lower primes). Thanks to the presence of complex numbers and something called superposition of particles, QCs also play a strong role in solving probability problems, predicting certain phenomena and sophisticated data analysis (QML).
The mass implementation of QC solutions is somewhat hampered by the technological development itself. Quantum computers will become really useful only when working with millions of physical QUBITs. With this quantity, it is possible to provide enough logical QUBITs that algorithms (like Shore, see below) need. However, since it must be maintained that QUBITs do not interact with each other and retain value for long enough time, technology is still struggling with making 10 million different particles to “work conscientiously for the common cause.” According to data from Jack D. Hidara’s current book, we are a still quite a few steps from this useful zone (now featuring few tens of logical qubits only):
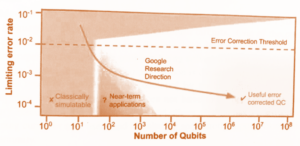
A certain complication for the development of QC solutions is that in order to confirm the functionality of the algorithm on QC, one must (usually) perform a simulation of this process on a classical computer. However, since QUBIT needs approximately 4000 times more data space than 1 BIT on a conventional PC to store its states, a complete simulation of only 30 QUBITs would take up all of your Notebook memory. The thousands to millions of QUBITs that are really needed are out of question even with the world’s most supercomputers. To quickly compare, how much memory space (to simulate QC QUBITs) is needed, have a look at a neat overview from aforementioned book:
Sectors most affected by QC
We looked quite in detail at the difference between QC and their classic PC predecessors. However, we have not yet mentioned which areas of human life are most suitable for the introduction of QC. Some indication flashed with revealing that QCs have the mightiest power in tasks where CCs need to remember large data structures or where the complexity of classical computational algorithms is quadratic and higher. Probably the most straightforward impact of QC is on cryptography, or encryption. The safest ciphers currently rely on huge prime numbers that cannot be easily detected. On a classic computer, you need to try a large number of divisions (by smaller primes) to see if a number is a prime or not. The brute force of classical computers makes these ciphers unbeatable. You won’t be able to find the prime number you need while the password is in effect. However, QC is able to find, using Shor’s algorithm, prime factor decomposition much faster and thus break the (even today) super-safe ciphers with brute force. It is important to say that this is a double blow for cryptography. Not only can it break the current super-strong passwords, it also deprives cryptography of the way it resisted so far: Whenever current cryptographic keys became vulnerable to breakthroughs, the encryptors simply doubled their length and everything went beyond the old way again. However, the problem is that the computational complexity of QC key breaking only increases logarithmically, so even if a breaking of 10-digit password lasted a day, the 1000-digit break would only take 3 days and a million-digit password break would only last 6 days (approximate values to illustrate, in reality natural not decimal logarithm is applied). Thus, even a drastic jump from a 10-letter password to a million-letter password will not bring you much more protection.
The second area where the advent of quantum computers is unstoppable is chemistry, biophysics and pharmacy. Quantum computers are a great help in testing a large number of molecules in pharmacy. They are able to check much faster what combinations of substances achieve the desired effects, or which of the proteins have the greatest (statistical) predisposition to react in the way we need to achieve. Research in these areas will rapidly accelerate through QC, bringing more discoveries of active substances to medicine (and compound materials for industry).
A separate branch of QC future is the data analysis process that has “crawled” into all sectors of our company in the meantime. That’s also reason why I decided to popularize QC on this blog. Not only are quantum computers able to efficiently sort products (product recommenders) using Grover search, but especially the classification algorithms (Quantum Machine Learning) and QNN (quantum neural networks) are also progressing significantly. QC-based sampling algorithms are also very useful in statistics and data analysis, as unlike conventional quasi-coincidence randomness, quantum computers can generate real random numbers.
Although not yet confirmed by specific solutions, by the nature of the QC specifics, it is evident that quantum computers will also be used to manage the coordination of a large number of people and/or things. Working with huge matrices is a piece-of-cake for QC. It is thus clear that quantum computers will have a significant impact on (analysis and management of) telecommunications and social networks, transport or production. Similar models can be used for more detailed sociological and marketing analyses and simulations. Even early suggestions for using QC in high-frequency stock trading appeared, but I haven’t even noticed a comprehensive prototype in the expert literature yet. As the number of sectors into which QC “bites” is not small, it is advisable to consider the heading of the next paragraph:
Do we have to (re)learn to work with QC?
From the previous paragraph, you know that it is quite unlikely that we should (at least in the foreseeable future) replace our desktop computers with quantum computers. It is much more likely that, if we use quantum computers by chance, it will be remotely over the Internet (read as cloud). It is a bit analogous to operating a video drone, which also shoots video, just like a classic camera, but you also don’t fly in the air with the drone to actually shoot the video, but you control the drone remotely from the ground. Thus, a group of professions (such as QC engineer) will need to rise to keep quantum computers running, but most ordinary users will issue orders to quantum computers over distance.
That also means that you can take advantage of quantum computing, even if you may not understand quantum physics behind it. (Therefore, it is incomprehensible to me why most QC descriptions already kill readers on the second or third page of QC explanation by some ugly equations, discouraging them from reading on.) It is a bit like becoming a programmer: Wanna-be coders (probably still) have to go through Assembler, a binary programming language course, in which the tiny components of CC speak to each other. This programming language is called low-level, since it can be used directly at the lowest level (on BITs). Most operating systems of recent PC’s will not allow you to go “as deep” as issuing commands directly to micro components, as conventional processors have approximately 2 billion in action at the same time. (For better comprehension, hundreds of millions in area of your nail size). Giving orders directly to 2 billion parts is unthinkable for man, simply by design. Therefore, IT professionals have created an environment for us that is “high” above the level of the electronic circuits themselves. Similarly, with quantum computers: At the time of QC mass expansion, nobody will work directly on the quantum circuit level. High-level languages such as LIQui|>, Qiskit, Q#, Quipper, Cirq, Scaffold or ProjectQ will be used. Most of these languages are powered by Python, Java or C ++, so if you’re already working with data, switching to QC won’t be as big a jump as it may look.
The second important fact for the future is that QCs may not replace conventional computers, but rather complement them. Same way as more powerful graphics card, that you need to purchase in order to edit video or plot 3D architectural models. As mentioned before, Quantum computers will probably be controlled remotely, and how otherwise we would be able to control them than from a classic computer? From the nature of quantum computing, it does not make sense, e.g. to connect a monitor to the QC unit. Displaying the results of QC calculations is not very visually intuitive. (Often this is a multi-dimensional space that our 3D perception somehow does not swallow). Although it should be fairly acknowledged that it took decades to get to the monitors attached even to classical computers (Yes, you may not believe, but all the outputs were first on punch cards). So one day we may find a way to intuitively display QUBITs, maybe. For now, though, the results of the QC calculations are sent back to a standard computer that stores or displays them. Therefore, as far as we can see ahead, it looks more like a dual-horse-carriage QC + CC, rather than an invasion of stand-alone QC computers.
What does that mean for me?
If you have read this far, surely the thought of what all this means to me is whirling in your head. If we summarize the conclusions from different points of this blog into one summary, we shall arrive at:
a] Quantum computers will succeed in a relatively large number of industries for the future.
b] However, they are not a universal substitute for computers as we know them now. Most likely in the future, humanity will have systems that will be a combination of QC + CC.
c] If you are an ordinary office worker using a computer today, you may not need to relearn to work with QC again. However, if you happen to know how to use it, QC is a career opportunity for you. Assumption is it will be wanted in 5-7 years.
d] If you are a data analyst, researcher, or other profession that collects and evaluates large volumes of data (see industries above), you will have less of the choice. QC can indeed be a threat to you. Because a combination of QC + CC solutions is more than likely to appear in your working environment. If you don’t have “a clue” about QC principles, you can become less of an asset on the labor market.
e] Fortunately, the principles of quantum computers and their applications are easy to understand, even if you do not have a degree in Theoretical Physics or Mathematics. If you want to get ready for QC, I would suggest to start familiarizing with types of algorithms that are much faster on QC than on conventional computers. (However, you will need to study the different reversible operations that are possible on QC as prerequisite to understand how these algorithms work. This may not be necessary easy reading.) At the same time, I suggest to study integration of at least one of the aforementioned QC programming languages (e.g. Cirq) with Python.
For those really excited about the topic, I attach a few books where they can begin their knowledge-hunt journey. At the same time, I would like to remind each reader to leave feedback (via info@mocnedata.sk) about whether this blog helped you to understand what quantum computers are. Thank you in advance.
Suggested reading:
Jack D. Hidary: “Quantum computing: An Applied Approach“
Chris Bernhardt: “Quantum Computing for Everyone“
Robert S. Sutor: “Dancing with Qubits: How quantum computing works and how it can change the world“
Publikované dňa 5. 3. 2020.
Späť na domovskú stránku
